RD Sharma CBSE Class 10 Chapter 6 Trigonometric Identity EX 62 Q 6 If 1/√3 cos theta sin theta =2/√3 , then the value of theta in circular measure is (A) π/2 (B)π/3 π/4 (D)π/5= √2 2 Find the value of cos 330° Solution cos 330° = cos (270 60)° = sin 60°;
How To Find Theta For Cos Theta 1 2 Quora
Cos 3 theta/2cos2theta-1=
Cos 3 theta/2cos2theta-1=-Find the General Solution of the Following Equation Cos X = − √ 3 2 Mathematics Shaalaacom1 sinθ − 3 cosθ = cosθ − sinθ 3 sinθ cosθPutting 1 = r cosϕ and 3 = r sinϕ, we get∴ r = 1 3 = 2 and tanϕ = 3 1 = tanπ 3⇒ ϕ = π 3∴ 1 sinθ − 3 cosθ = r cosϕ cosθ − r sinϕ sinθ sinθ cosθ= 2 r ( cosϕ cosθ − sinϕ sinθ) 2 sinθ cosθ= 22 cos( ϕ θ) sin2 θ = 4 cos( π 3 θ) sin2 θ




2 Cos Squared Theta Minus Under Root 3 Cos Theta Is Equal To Zero Find The Theta Brainly In
Trigonometric Functions are formed when trigonometric ratios are studied in terms of radian measure for any angle (0, 30, 90, 180, 270)These are also defined in terms of sine and cosine functions In this article, we will provide you with all the details on trigonometric functions such as value in degree, radians, complete trigonometric table and other relevant information The measure of angle(theta) Is 2pi/3, which statements are true?If sin theta = √3/2 as shown above, then theta = 60° as can be obtained from a trigonometric table So, to calculate tan (90theta)° or to find tan 90°60° or tan 30°, it is available from the trigonometric table and it is (√3)/3
Click here👆to get an answer to your question ️ Solve 2 cos^2theta √(3)sintheta 1 = 0If cos θ sin θ = √2 cos θ, prove that cos θ sin θ = √2 sin θ Get the answer to this question and access more related questions along with answers hereIf $\sin^2 \theta 2\cos \theta – 2 = 0$, then find the value of $\cos^3 \theta \sec^3 \theta$ Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers
A)cos theta B)cos theta C)sin theta D)sin theta my book doesnt give examples of this but my crack at it would be C b/c distributive property?Let cos(theta) = x, sin(theta) =x sqrt(3) then 1=sin^2(theta)sin^2(theta)= 4x^2 Therefore cos(theta)=x=1/2 (and sin(theta)=sqrt(3)/2)or cos(theta) = x=1/2 (and sin(theta)=sqrt(3)/2) 1) Write counting from 0 to 4 2) Divide all the numbers by 4 and simplify these numbers 3) Taking square root of all these numbers 4) The values we get are the values on the sin function at different standard angles For values of other trigonometric ratios




How To Write Exact General Solution Sinx Sqrt 3 2 For Trigonometric Equation Youtube




If Sin Theta 2 A Cos Theta 2 B Then 1 Sin Theta 3sin Theta 4cos Theta 5
And 2cos theta = sin theta You can view more similar questions or ask a new question Let cos(theta) = x, sin(theta) =x sqrt(3) then 1=sin^2(theta)sin^2(theta)= 4x^2 Therefore cos(theta)=x=1/2 (and sin(theta)=sqrt(3)/2)or cos(theta) = x=1/2 (and sin(theta)=sqrt(3)/2)First week only $499!
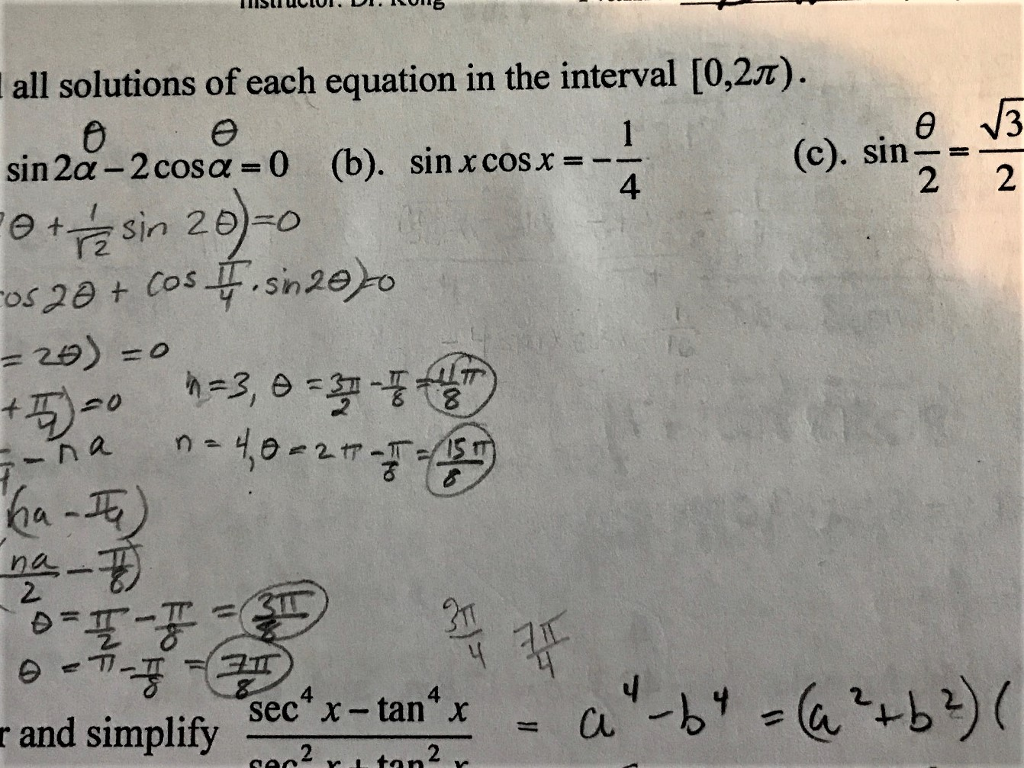



Find All Solutions Of Each Equation In The Interval Chegg Com




If Sin 2 Theta 3 Cos Theta 2 Then Find Value Of Cos 3 Theta Sec 3 Theta
$$ =\cos ^3 \theta 3 \cos ^2 \theta \cdot i \sin \theta 3 \cos \theta \cdot i^2 \sin ^2 \theta i^3 \sin ^3 \theta $$ To find $ \cos 3 \theta $ equate real parts (first and third terms ) and to find $ \sin 3 \theta $ equate imaginary parts (second and fourth terms) We can recognize such derivational origin by polynomial approach right awayClick here👆to get an answer to your question ️ Solve √(3)costheta 3sintheta = 4sin 2thetacos 3theta Join / Login >> Class 11 >> Maths >> Trigonometric Functions >> Trigonometric Equations Question Solve 3 cos θ − 3 sin θ = 4 sin 2 θ cos 3The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are (), (), and (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, and , if an interpretation is unambiguously possible The sine of an angle is defined




The Principal Solution Cosx Sqrt 3 2 Is



How To Solve The Following Trigonometric Equations 3 Cos 8 3 2 Sin 28 3 Cot 2 8 1 0 Quora
√3/2 Sin 30° and Cos 60° 1/tan thetdjacent 1/x on unit circle cos's sister difference between graph of sin and graph of cos sin passes through the origin cos does not periodIf sin theta = sqrt(3) / 2 What does cot theta equal? How do you find all the solutions for #2 \sin^2 \frac{x}{4}3 \cos \frac{x}{4} = 0# over the




If 3 Tan Theta 4 Evaluate 3sin Theta 2 Cos Theta 3 Sin Theta 2 Cos Theta Youtube




Solve Cos X Sqrt 3 2 Youtube
Determine the exact value of sin(θ)cos(θ) if csc(θ) = 3 and (θ) is in Quadrant II Draw a triangle Opposite side is 1, hypotenuse is 3, adjacent side is 2 \sqrt2 Find sin,cosNote the signs , respectively Draw a triangle By using the value of cosine function relations, we can easily find the value of sin 1 degrees Using the trigonometry formula, sin (90 a) = cos a, we can find the sin 1 value We know that the value of cos 30 degrees is √3/2 Therefore, sin 1° = √3/2 ←In the case where 1 − η 2 (1 − cos 2 θ) < 0 1\eta^2(1\cos^2\theta) < 0 1 − η 2 (1 − cos 2 θ) < 0, we have total internal reflectionin this case you return false and the wi field is unused




If 4 Cos 2theta Sqrt 3 2 Sqrt 3 1 Costheta Then Theta Is A 2npi Pi 3 N In I B 2npi Pi 4 N In I C 2npi Pi 6 N In I D None Of These




2 Cos Squared Theta Minus Under Root 3 Cos Theta Is Equal To Zero Find The Theta Brainly In
NEED TO KNOW FOR EXAM!!2cos(theta)3=2 Move all terms not containing to the right side of the equation Tap for more steps Subtract from both sides of the equation Subtract from Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor ofCos(theta) = √3/2 The measure of the reference angle is 30° The measure of the reference angle is




Misc 9 Cos X 1 3 Find Sin X 2 Cos X 2 And Tan X 2




If Cos Theta Sqrt 3 2 Then Find The Value Of 1 Sec Theta 1 Cosec Theta Youtube
You can put this solution on YOUR website!Learn with flashcards, games, and more — for freeR p = (η 2 k 2 ) cos 2 θ i 2 η cos θ i 1 (η 2 k 2 ) cos 2 θ i − 2 η cos θ i 1 where η \eta η and k k k are used together to represent indices of refraction for conductors Both of them are Vector3D values, recording the scalar η \eta η and k k k values at wavelengths 6 1 4 614 6 1 4 nm (red), 5 4 9 549 5 4 9 nm (green



If Cos Theta Sqrt 3 2 Then What Is The Value Of Theta Youtube




Solution Of Equation 3 Cos 2 Theta 2 Sqrt 3 Sin Theta Cos Theta 3 Sin 2 Theta 0 Are M Frac Pi R And M 0 3 0 Circ 7 109 Frac 15 5 Then Mathrm R Mathrm S
(i) If sin θ cos θ = √3, then prove that tan θ cot θ = 1 (ii) If √3sin θ cos θ = 0, then show that tan3θ = (3tanθ tan^3θ)/(1 3tan^2θ)Sin theta = 1/2, cos theta = sqrt(3)/2 Trigonometric Identities (1) Conditional trigonometrical identities We have certain trigonometric identities Like sin2 θ cos2 θ = 1 and 1 tan2 θ = sec2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called




0 Lt Theta Lt Pi 2 2sin Theta Sqrt3 Cos 10 Sin 10 Gt Theta I 50 0 Ii 70 0 Iii 40 0 Iv 80 0




If Sintheta A A 2 B 2 0 Theta 90 O Find The Values Of Costheta And Tantheta
Given cos θ = \(\frac{\sqrt{3}}2{}\) Since, θ is in IIIrd Quadrant So, sin and cos will be negative but tan will be positive We know that, cos 2 θ sin 2 θ = 1 Putting the values, we get Since, θ in IIIrd quadrant and sinθ is negative in IIIrd quadrantIf the radius of a sphere is increased by 4 cm, its surface area is in;COMEDK 08 √2 √22 cos4θ (A) cos θ (B) 2 cos θ cos 2 θ (D) 2 cos 2 θ Check Answer and Solution for above question from Mathematic




Find The General Solution For The Equation 3 Cos Theta Sin Theta 2 Maths Trigonometric Functions Meritnation Com



How To Find Theta For Cos Theta 1 2 Quora
The Radius Of The Circle With The Polar Equation R 2 8r Root 3 Cos Theta Sin Theta 15 0 Is The radius of the circle with the polar equation r 2 8r(√3 cos θ sin θ) 15 = 0 is 1) 8 2) 7 3) 6 4) 5 Solution (2) 7Given cos theta = 1/3 and theta in Quadrant IV, find tan theta close Start your trial now!Given, cos theta = 21/29 We know that sin^2 theta=1cos^2 theta Hence (sin theta)^2 = 1(21/29)^2 → sin theta = /29 or /29 Depending on the quadrant in which theta lies we will select the sign, ie if theta lies in first or second quad then sin theta = /29 and if theta lies in third or fourth quad then sin theta = /29 Hope you got it




Ex 3 2 1 Find Values Of Other Five Trigonometric Functions If Cos X




Principal Solution Of Cos X 3 2 Brainly In
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorArrow_forward Question A Let, √(35i) = √x i√y Square both side (√(35i))2 = (√xi√y)2 3 5i = xयदि एक गोले की त्रिज्या 4 सेमी बढ़ जाती है, तो इसका पृष्ठीय क्षेत्रफल




If Cos Theta Sqrt 3 2 And Theta Lies In Quadrant Iii Find The Values Of All The Youtube




04 Si Cos 8 Frac Square Root Of 23 Calcula Gauthmath
If sin x sin y = a and cos x cos y = b then value of sin x sin y cos x cos y is Q11 There are two temples, one on each bank of a river just opposite to each otherRelated Questions यदि cos θ = 1/√5, जहाँ 0 θ \(\frac{{2\tan \theta }}{{1 {{\tan }^2;So ∠B = sin(1)√3/2 = 60° sinBCD = BD/CD ⇒ 1/√3 So ∠BCD = sin (1)1/√3 ⇒ 30° So when sine of an angle is √3/2, it is a right triangle whose hypotenuse is 2 units, opposite side is √3 units and adjacent side is 1 unit, Taking this into consideration you can find out ratios of cosθ, tanθ and cotθ when sinθ is √3/2 cosθ = 1/2




Example Find Solution Of Sin X Root 3 2 Class 11




Solving Trig Equation Of Cos X 3 2 Youtube
Learn how to solve integrals of rational functions problems step by step online Find the integral int(1/((a^2x^2)^(3/2)))dx Simplifying We can solve the integral \int\frac{1}{\sqrt{\left(a^2x^2\right)^{3}}}dx by applying integration method of trigonometric substitution using the substitution Now, in order to rewrite d\theta in terms of dx, we need toSince we know, cos (270° θ) = sin θ = \(\frac{√3}{2}\) Trigonometric Functions Basic Trigonometric Ratios and Their Names;A is opposite to A, b opposite B, c opposite C a/sin (A) = b/sin (B) = c/sin (Law of Sines) c ^2 = a ^2 b ^2 2ab cos b ^2 = a ^2 c ^2 2ac cos (B) a ^2 = b ^2 c ^2 2bc cos (A) (Law of Cosines)




If Cos Theta Is Equal To Root 3 By 2 Then Find The Value Of 1 Minus Sec Theta Divided By 1 Cosec Brainly In




हल क ज ए Tan Theta Sec Theta Sqrt 3 Youtube
Eg 1 cos 30° = 1 Cos 30° = 1 x √3/2 = √3/2 And cos θ = 1/sec θ Or, sec θ = 1/cos θ Also, sin (90 θ) = cos θ and Cos (90 θ) = sin θ Also remember sin 45 = cos 45 = 1/√2 The value of sin θ and cos θ can never be greater than 1Sin theta=√3/2 theta=π/3 cos theta=cos π/3=1/2 cot theta=cos theta/sin theta=1/√3=√3/3Restrictions of Trigonometrical Ratios




Prove Cos 1 X Cos 1 X 2 Root 3 3x 2 2 Pi 3 Teachoo




Ex 3 2 1 Find Values Of Other Five Trigonometric Functions If Cos X
180° π1 150° 5π/6√ 3 /2 135° 3π/4√ 2 /2 1° 2π/31/2 90° π/2 0 60° π/3 1/2 45° π/4 √ 2 /2 30° π/6 √ 3 /2 0°Sinθ cosθ = √2 \(\frac{1}{{\sqrt 2 }}{\rm{sin\theta }} \frac{1}{{\sqrt 2 }}{\rm{cos\theta }} = 1\) sinθ \( = \frac{1}{{\sqrt 2 }}{\rm{\;and\;cos\theta3/1 4/0 Given Triangle abc, with angles A,B,C;



Cos X Sqrt 3 2 Give The General Formula Solutions Youtube




If Cos Theta 1 2 And Pi Theta 3pi 2 Then Find The Value Of 4tan 2 Theta 3cosec 2 Theta
Note 1 cos theta = 1 Cos θ;What are the remaining trigonometric functions of theta when sin theta= square root 3/2, cos theta 0 ** When sin x =√2/3, and cos0, it means the reference angle is in quadrant II, where sin>0 and cos0 You are working with a right triangle where the opposite side=√2 and the hypotenuse=3




Area Inside Outer Curve Of Limacon R 1 2 Cos Theta Mathematics Stack Exchange




If 7 Sin 2 Theta 3 Cos 2 Theta 4 Then Show That Tantheta 1 3




If Cos Theta Minus Root 3 2 And Theta Lies In Quadrant Third Find The Values Of All Other Brainly In




Let F N Theta Cos Theta 2 Cos 2theta Cos 7theta 2 Cos 3n 2 Theta 2 Sin Theta 2 Sin 2theta Sin 7theta 2 Sin 3n 2 Theta 2 Then F 3 3pi 16




If Root 3 Sin Theta Is Equal To Cos Theta Find 3cos Square Theta 2cos Theta Divided By 3cos Theta 2 Brainly In




If Costheta 3 2 And Theta Lies In Quadrant Iii Find The Values Of All The Other Five Trigonometric Functions



2 Solve Cos 8 Square Root Of 3 2 On 8 Gauthmath




The Value Of Theta Satisfying The Given Equation Cos Theta Sqrt 3 Sin Theta 2 Is A Pi 3 B 5 Pi 3 C 2 Pi 3 D 4 Pi 3



3




The Value S Of Theta Which Satisfy 3 2costheta 4sintheta Cos2theta Sin2theta 0 Is Are




If Sin Theta Sqrt 3 2 Then Cosec Theta Cot Theta Youtube




The Principal Solution Cosx Sqrt 3 2 Is Youtube




If Tantheta 1 Sqrt 3 Sintheta 1 2 And Costheta Sqrt 3 2 Then The Principal Value Of Theta Will Be



If Cos 8 3 2 And Sin A 3 5 Where 0 Does Not Lie In The Third Quadrant Then Sarthaks Econnect Largest Online Education Community



What Is The Sin 1 Sqrt 3 2 Socratic




Example 6 If Cos X 3 5 X Lies In Third Quadrant Find




Csc 8 3 2 Tan 8 Square Root Of 3 Sec Gauthmath




Misc 2 Find Values Of Theta P If Equation Is Normal Form



What Is The Value Of Tan Theta If Sin Theta Cos Theta Root 2 Cos Theta Quora
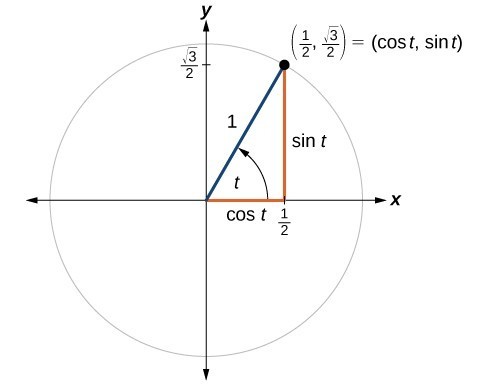



Unit Circle Sine And Cosine Functions Precalculus Ii




If Sqrt 3 Sin Theta Cos Theta Find The Value Of Frac 3 Cos 2 Theta 2 Cos Theta 3 Cos Theta 2




Rd Sharma Solutions For Class 10 Chapter 5 Trigonometric Ratios Exercise 5 1 Get Pdf For Free




If Sin Theta 1 2 And Cos Theta Root 3 2 Then Find The Value Of Tan Theta Tan Theta 1 Minus Tan Brainly In
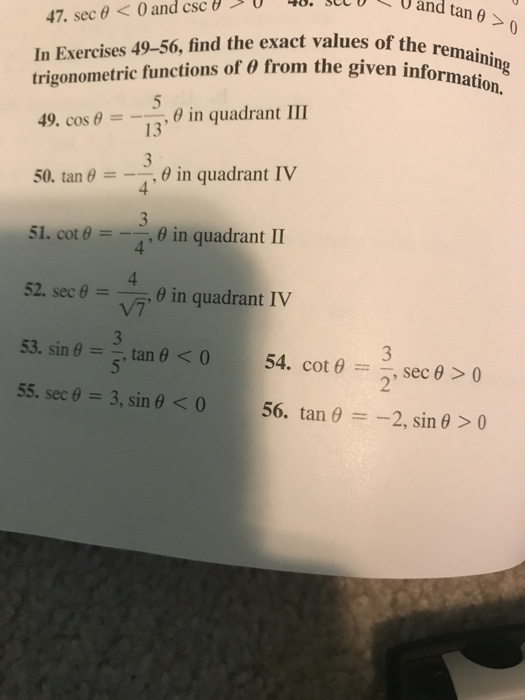



Find The Exact Values Of The Remaining Trigonometric Chegg Com




Cos 2 Theta Square Root 3 2 Cos 2 Theta Chegg Com




Ex 2 1 2 Find Principal Value Of Cos 1 Root 3 2 Class 12



1
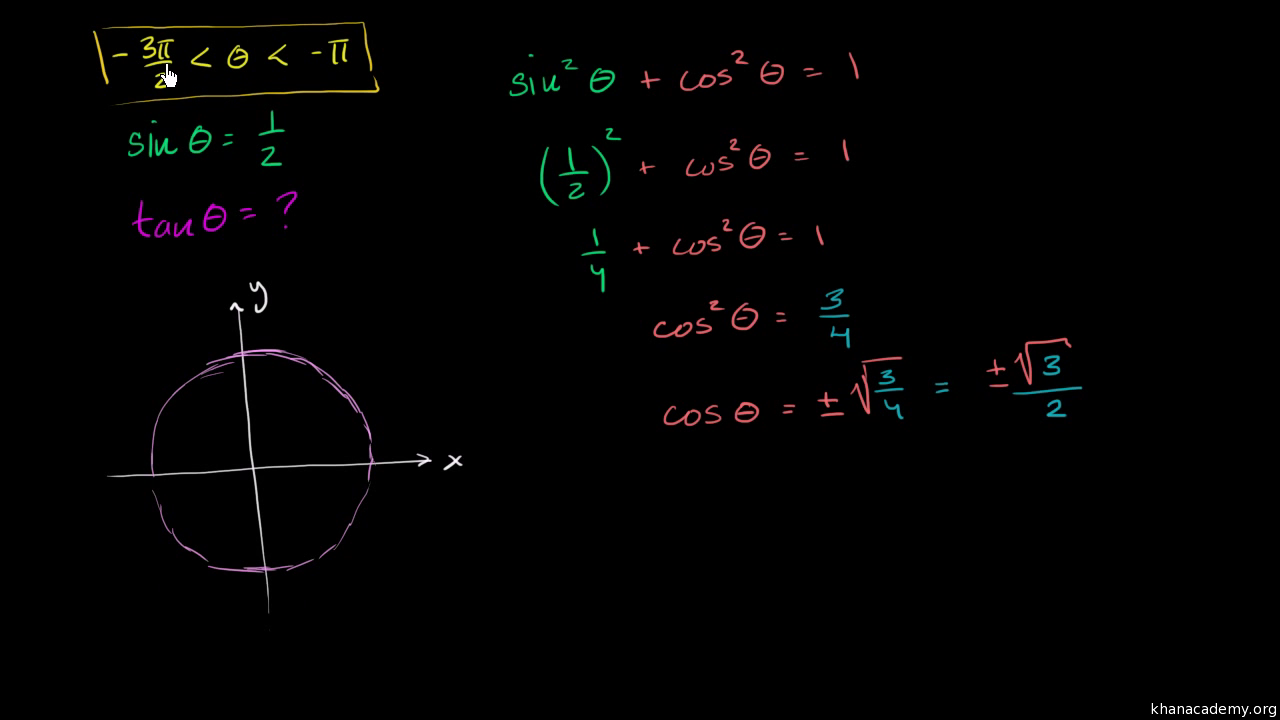



Using The Pythagorean Trig Identity Video Khan Academy




Find All Solutions Of The Following Equations Between Chegg Com




If Cos Theta Is Equal To Root 3 By 2 Then Find 3 Sin Theta 4 Sin Cube Theta Is Equal 1 Brainly In




Sin Theta Sqrt 3 2 Cos Theta 1 2 Youtube



1



How To Evaluate 8 For Cos 8 3 2 If It Is Between 0 And 2pi Quora




How Do You Simplify Cos 2 Pi 3 Socratic



What Is The Principal Value Of Cos 1 3 2 Sarthaks Econnect Largest Online Education Community



What Is The Solution To Sinx Cosx 3 2 Quora




If Cos Theta Sin Theta Sqrt 2 Cos Theta Prove That Cos Theta Sin Theta Sqrt 2 Sin Youtube




Solve For X 4 Cos 2 X 3 2 3 1 Cos X Brainly In




If Sin Theta 1 2 And Cos Theta Sqrt3 2 Then The General Value Of Theta Which Satisfie Youtube




If 2 Costheta 3 Then Find All The Trigonometric Ratios Of Angle Theta



What Is The Cartesian Form Of 2r 3 Theta Cot Theta Cos Theta Socratic



If Tan 8 3 4 Find The Values Of Sec 8 And Cos 8 Sarthaks Econnect Largest Online Education Community
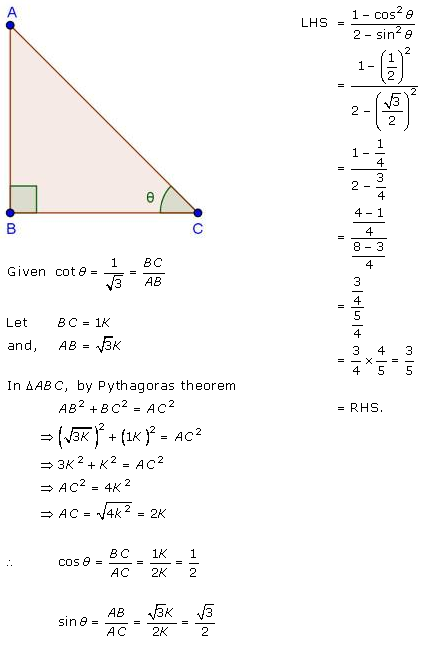



If Cot Theta 1 Root 3 Show That 1 Cos Square Theta 2 Sin Square Theta 3 5 Mathematics Topperlearning Com R01kexoo




If Sin Theta Cos Theta Root 3 Then Prove Thattan Theta Cot Theta 1 Brainly In




Given That Sin A 3 2 And Cos B 0 Then The Value Of B A Is
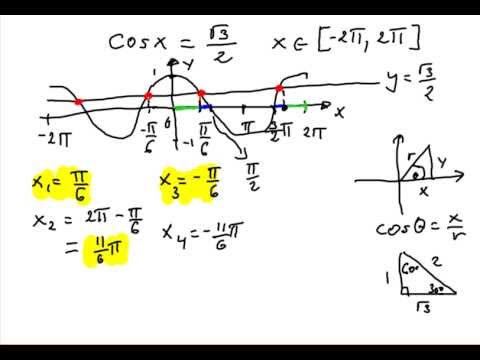



How To Solve A Trigonometric Equation When Cosx Sqrt 3 2 Part 5 Of 8 Youtube




Solve The Problem If Cos Theta 1 3 Theta In Chegg Com




If R Cos Theta 1 R Sin Theta Root 3 Then Theta Brainly In
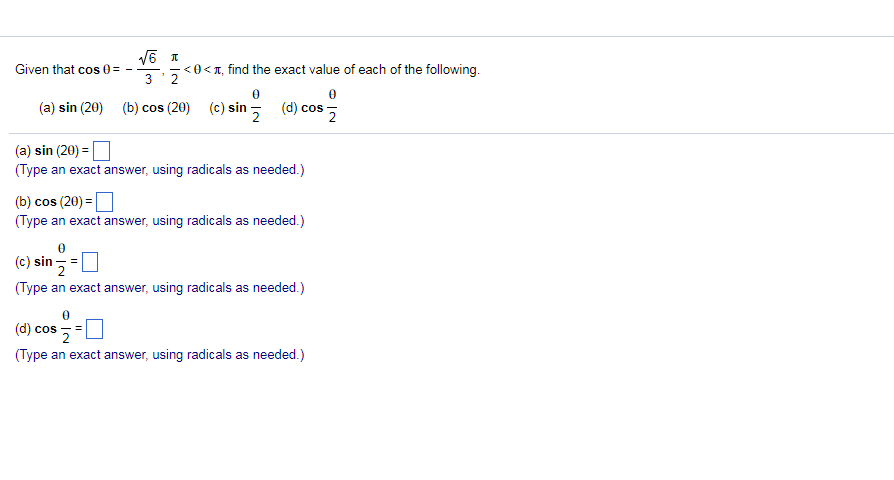



Given That Cos Theta Squareroot 6 3 Pi 2 Theta Chegg Com




If Sintheta 1 2a N Dcostheta Sqrt 3 2 Then The General Value Of Theta Is N In Z Dot A 2npi 5pi 6 B 2npi Pi 6 2npi 7pi 6 D 2npi Pi 4




Find All The Values Where Cos Theta Sqrt 3 2 Youtube




If Cos Theta 3 5 And Pi Lt Theta Lt 3pi 2 Find The Value Of Sec Theta Tan Theta Cosec Theta Cot Theta




Trigonometry




If 3 Sin 8 Cos 8 0 And 0 8 90 Find The Value Of 8 Video




5 Given That Cos 8 3 O And P 2 8 P Find Each Chegg Com




If Sin Theta 3 2 Find The Value Of All The Trigonometric Ratios Of Theta Brainly In




Solve Trigonometric Equation 3 1 Cos X 3 1 Sin X 2 Youtube




If Cos Theta Is Equal To 2 Upon 3 Find The Value Of 2 Sec Square Theta 2 Tan Square Theta Minus 9 Brainly In




If Y 2sintheta 3 Costheta Then The Minimum Value Of Y Is




If X 3 Cos Theta 2 Cos 3 Theta Y 3 Sin Theta 2 Sin 3 Theta Then Dy Dx Is




If Sin Theta Cos Theta Sqrt 2 Then Tan Theta Youtube



Q Tbn And9gcswsf Ecpsduz38bfjvi Leyscrwp8sy42we07iguooyebhgdbn Usqp Cau




If Cos Theta 3 5 Find The Value Of 5 Cosec Theta 4 Tan Theta Secth Youtube



Cos Theta Equals 0 General Solution Of The Equation Cos 8 0 Cos 8 0




Rd Sharma Solutions For Class 10 Chapter 5 Trigonometric Ratios Exercise 5 1 Get Pdf For Free




Root 3 Sin Theta Minus Cos Theta Is Equal To 2 Solve It Brainly In




Given Sin Theta Square Root 3 3 And 3 Pi 2 Chegg Com
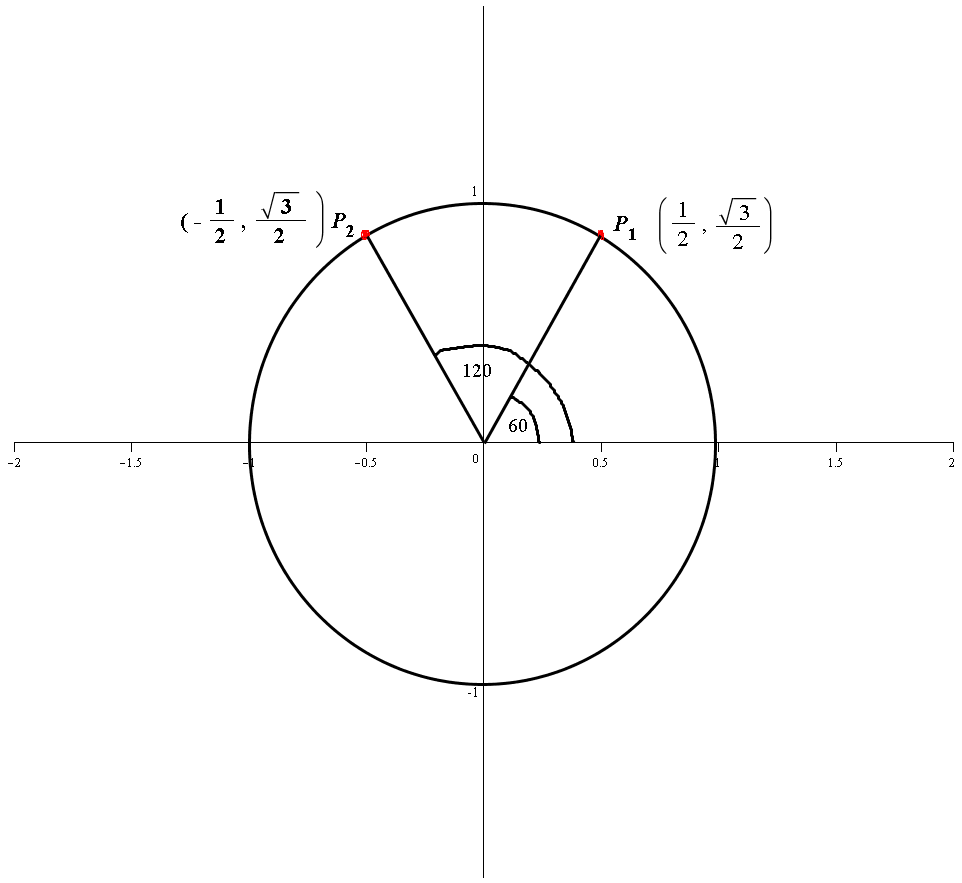



If The Point X Sqrt 3 2 Is On The Unit Circle What Is X Socratic




If Cos Theta Is Equals To Root 3 By 2 Then Find 4 Sin Square Theta Tan Square Theta Brainly In




Misc 9 Cos X 1 3 Find Sin X 2 Cos X 2 And Tan X 2




If Cos Theta Root3 1 2 Root 2 And Sin Theta Root3 1 2 Root 2 Then What Is The Arguement Maths Complex Numbers And Quadratic Equations Meritnation Com




If 2sin Theta Pi 3 Cos Theta Pi 3 And Tantheta 3 0 Find The Value Of Theta
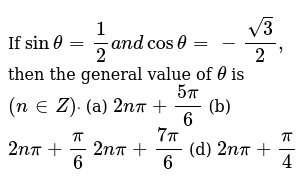



If Sintheta 1 2a N Dcostheta Sqrt 3 2 Then The General Value Of Theta Is N In Z Dot A 2npi 5pi 6 B 2npi Pi 6 2npi 7pi 6 D 2npi Pi 4
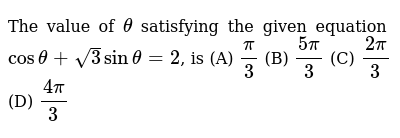



The Value Of Theta Satisfying The Given Equation Cos Theta Sqrt 3 Sin Theta 2 Is A Pi 3 B 5 Pi 3 C 2 Pi 3 D 4 Pi 3



0 件のコメント:
コメントを投稿