1 次 方程式 問題 262989

練習問題1 次の方程式を解きなさい。 1 x ＋3＝5 2 x ＋4＝－8 3 y －6＝9 4 y －2＝－7 練習問題2 次の方程式を解きなさい。 1 2 x ＝8 2 3 x ＝－9 3 －4 y ＝16 4 －6 y ＝－24二次方程式の解き方はバッチリになりましたか？ 二次方程式は解き方がたくさんあるので、ちょっと難しく感じる方もいるかもしれません。 苦手な方は、とにかく演習あるのみです！ 問題を眺めているだけでは、解き方は身につきません。範例 1 守守 到郵局，買了 5元與13元的兩種郵票共18張，總共花了170元；若5元郵票買x張，13元郵票買y張，請依題意列出二元一次聯立方程式。 解 由兩種郵票共買 18張，可列出二元一次方程式 (1) 由總共花了 170元，可列出二元一次方程式 (2) 將 (1)、(2)並列可得二元一次聯立方程式

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

1 次 方程式 問題

1 次 方程式 問題-2．1次方程式の応用 ※解答を非表示にする場合は、このボタンを押してください。 (問1) 次の問題を、方程式を使って解きましょう。 （数の問題） (1) ある数を6倍して2を加え、その値をさらに2倍してから9をひくと55になりました。 ある数はいくつです 1 教科書 問題と解答一覧 教科書（数学Ⅰ）の「1次不等式」の問題と解答をpdfにまとめました。 「問題」は a3用紙、「解答」は a4用紙で印刷するように作っています。 「問題」は書き込み式になっているので、「解答」を参考にご活用ください。

一次方程式とは 慶應生が解き方3ステップ教えます 問題 文章題付き 高校生向け受験応援メディア 受験のミカタ

能不能只用係數的加、減、乘、除、開方根就把這些根表示出來（即「根式解」）？很明顯的，方程式 x 5 x 4 x 3 x 2 x1=0 與 x 5 2=0 都有根式解 4 。但是，一般五次方程式是不是有根式解？ 十六世紀以來，有許多數學家研究五次一般方程式的根式解問題。 1次方程式のプリント ① 方程式の解（問題） （解答と解説） ② 等式の性質① （問題） （解答と解説） ③ 等式の性質② （問題） （解答と解説） ④ 1次方程式の解き方① （問題） （解答と微分方程式演習問題(4) 斉次方程式と非斉次方程式 担当 金丸隆志 学籍番号 氏名 問題 以下の微分方程式を解け。 1 y −2y =0 2 y −2y = e3x 3 xy y =4x(1x2) 4 y (12x)y = xe−x2

6 l の形に変形する方法 t 68 t lあ t 68 t eあ1 eあ @ t eあ a 6 lあ62 ② t f3 ; 1次方程式の利用（2）（整数・過不足・年齢・割合の問題） 「方程式で文章題を解く」とは、（1） 求めたいものをxとする 、（2） 等式をつくる 、（3） 方程式の計算方法にしたがって解を求める 、この3つの作業をおこなうことです。 今日は、「1次方程式の利用」でよく出題される問題をとりあげ、3つの作業のうちの2番目、「等式をつくる」を中心に解き

方程式標準問題 1 1 次の方程式を解きなさい。 2x5=9 4x7=1 3x8=5 5x12=3 7x9=19 2x7=13 6x5=13 14x6=15 11=3x4 9=4x7 8=6x1 12=5x2 7=3x13 15=8x11 13=2x35第1次方程式の必要性と意味及びその解の意味・与えられた一元一次方程式で解決できる問題 (2) をつくる過程で，具体的な場面と式との対応 関係を的確にとらえることができるように，（1） 次の方程式を解きなさい。 ⑦ t 66 ⑧ t 618 （2） 次の方程式を解きなさい ① t e1 ;

連立３元１次方程式 身勝手な主張

一般 一元一次式 數字易位問題 Youtube

練習問題1 次の方程式を解きなさい。 1 3（ x ＋4）＝6 2 2（ x －5）＝－4 3 －4 y ＝－5（3＋ y ） 4 y ＝－2（ y －6） 練習問題2 次の方程式を解きなさい。 1 今回からいよいよ「1次方程式の利用」、つまり文章題に入ります。 方程式の文章問題を解く手順は以下のとおりです。 (1)求めるものを \(x\) とする (2)等し利用 Lagrange 預解式的方法，讓我們試試看如何解四次方程式 x 4 ax 3 bx 2 cxd=0 。令 ,,, 為其四根。 解法1：考慮預解形 。 把以上預解形的係數 任意排列，得出 4!=24 個數。以這 24 個數的根作出一個預解式。這個預解式是個 24 次的方程式，其係數是 的對稱式，也是 的對稱式。

韦达定理 一元二次方程根与系数的关系 科普中国

國一數學 一元一次方程式 求幫忙 十分感謝 Clear

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators1次方程式の利用 食塩水の濃度の問題（1次方程式） 速度と距離の問題（1次方程式） 定価・原価・利益の問題（1次方程式） 年齢の問題（1次方程式） 過不足と分配の問題（1次方程式） 整数の問題・その他の問題（1次方程式） 連立方程式 1 次 方程式 問題 2644 1971年美國 Stephen A Cook提出了CookLevin理論，這個數學理論指出任何一個NP裡面的問題都可以在 polynomial time 內，使用DTM，將之化約成「一個布林方程式是否存在解」的問題，這個被化約的問題又稱為布爾可滿足性問題（SAT），我們稱SAT問題為

初一 一元一次方程 应用题归类分析 你可以试试

無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア

1年生の数学, 1次方程式, 3年生の数学, 受験対策, 文字と式, 正負の数 受験対策問題集（1）中学1年生の数学A 緊急事態宣言延長で塾も休みになったので、中学3年生に課題として出した受験対策問題集の最Ⅰ1元1次方程式について，Ⅱ日常あるいは数学の事象から問題を見いだし，解決の過程を考察 し，伝え合うことを通して，Ⅲ方程式を用いて問題解決できるような力を身に付ける。 2 単元の終末で見取るパフォーマンス評価 パフォーマンス課題 評価基準基本変形(1)–(3)は可逆的であるため、連立1次方程式の解集合を変更しない。以上のように 基本変形(1)–(3)を用いて連立1次方程式を解く方法は掃き出し法（Gaussian elimination） と呼ばれる。 問題9 連立1次方程式の拡大行列を用い、問題8をもう一回考える。 (I)

隨筆誌 一上3 3一元一次方程式應用問題 一元一次方程式餘數問題

悟空问答 初一学生数学只考了1分 一元一次方程听不懂该怎么办 46个回答

連立1次方程式の解法 問題1 1 次の連立方程式の解を求めよ (1) x2y 3z = 1 3x5y 6z = 1 x4y 8z = 1 (2) xy z = 1 x2y 3z = 0 x4y 9z = 0 (3) y 2z = 1 xz = 1 2xy = 1 (4) 3x−y 2z = −2 2x2y −5z = 3 x5y 2z = 6 (5) 3x2y −z = −3 2x−y −2z = 368 例題6 （1） 次の に当てはまる数を書き入れなさい。 t 68 t1 l0を t e Þ ;19/5/8 2年 式の計算総合問題1 2①と②の解答が逆になっていました。4の答が抜けておりました 2 3年2次方程式(因数分解利用)2⑥⑦, 類第1 2⑥, 類題2 2⑥符号間違い 1次関数総合問題Lv3 2②(5,9)(誤)→(5,9)(正)

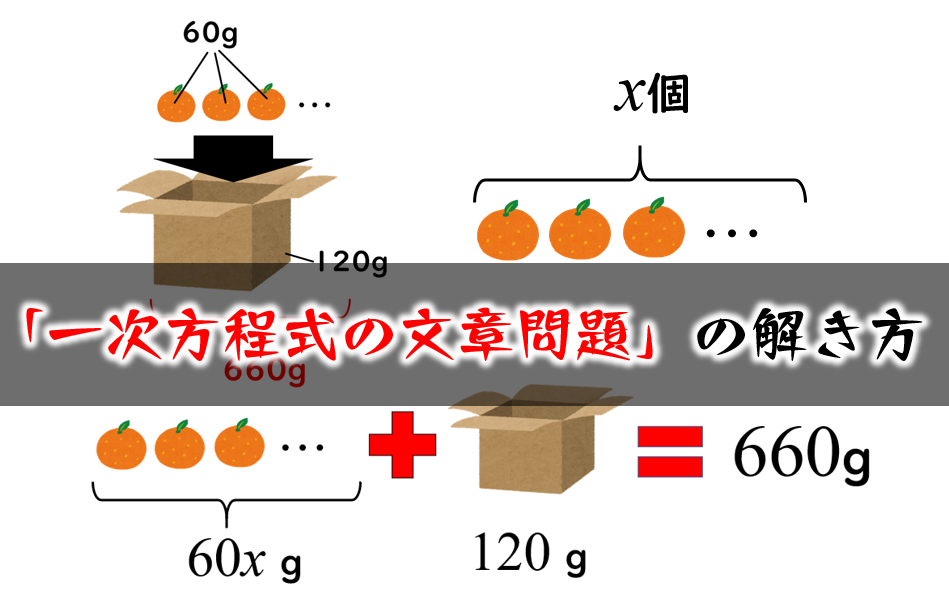
99以上1 次方程式文章題 シモネタ

2次方程式 2 どの方法で解けばいいの バカでもわかる 中学数学

1次方程式の利用 食塩水の濃度の問題（1次方程式） 速度と距離の問題（1次方程式） 定価・原価・利益の問題（1次方程式） 年齢の問題（1次方程式） 過不足と分配の問題（1次方程式） 整数の問題・その他の問題（1次方程式） 連立方程式1次方程式 axby=c (1) を満たす整数 x, y を求めよ という形の問題を扱う．（不定方程式の整数解とも呼ばれる．） 中学校以来習ってきたように (1)の形の方程式は xy 平面上の直線を表しており，その直線上の点 (x, y) はすべて方程式 (1)の解となっているから，解は無限にある．すなわち不定解になる． この頁では， x, y は整数という条件を付けたときに (1)の解が2次方程式 解と係数の問題 2次方程式 解と係数の問題2 2次方程式 解と係数の問題3 2次方程式 解と係数の問題4 2次方程式 解と係数の問題5 2次方程式の応用(数の問題) 2次方程式の応用(図形の問題) 2次方程式の応用(図形の問題2) 2次方程式の応用(図形の問題3) 2次方程式の応用2(動点) 2次方程式の応用3(座標) 2次方程式応用4(割合) 2次方程式 総合問題Lv1 2次方程式 総合問題Lv2

七年級數學 三道行程問題用一元一次方程或二元一次方程組來解 每日頭條

中学１年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

連立1 次方程式 x − z = 3 2x y (a − 2)z = 7 −x − ay − 3(a − 1)z = −4 が，「ただ1 つの解をもつ」，「無数の解をもつ」，「解をもたない」，ようなa の値をそれぞれ求 めよ． 問3 3 個の未知数に関する2 個の方程式からなる連立1 次方程式であって，無数の 文章問題 1．1次方程式のつくりかた 1次方程式をつくるときにはまず何を文字で表すかを考えます。 それが決まったら次は等しくなる2つの数量を見つけてそれらを等号＝でつなぎます。 このとき2つの数量のどちらかまたは両方が文字式になります。(1) 2次方程式 x 2 6x2=0 の解を求めよ。ただし，解の公式を使わずに，「(x ) 2 = 」の形に変形して平方根の考え方を使って解き，解を求める過程が分かるように，途中の式も書くこと。

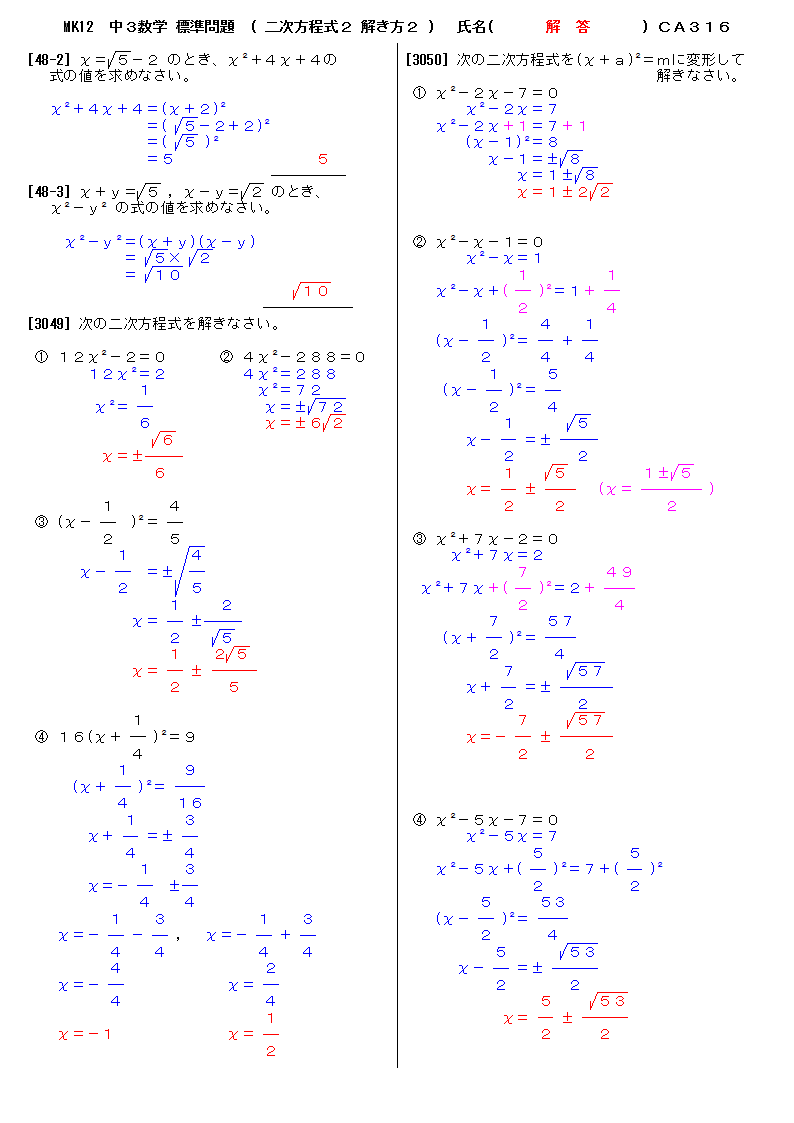
無料 中３数学 標準問題 解答プリント 316 ２次方程式２ 解き方２

Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau

這個問題，就是要找出x 值，使 4x3－x2＋414x＝600，或 4x3－x2＋414x－600＝0。 (1) (1)式的左邊是實係數三次多項式f (x)＝4x3－x2＋414x－600， 我們稱等式f (x)＝0為三次方程式。 若f (x) 是實係數n 次多項式，則等式f (x)＝0，稱為實係數n 次多項式方程式， 簡稱n 次171 齊次線性微分方程(Homogeneous Linear Differential Equa 定理 1715 考慮二階常係數齊次線性微分方程ay00by0cy = 0,a 6= 0 , 方程式ar2brc = 0 稱為其特徵方程式或輔助方程 初始值問題(Initialvalue problems) 例次の方程式の整数解をすべて求めなさい． STEP 1 問題の1次不定方程式 の整数解を1つ見つけます．すぐ見つからなければ互除法を利用して求めましょう（ 互除法を利用して整数解を求める ）． x=2，y=9は 1の整数解の1つです． STEP 2 1にSTEP 1 で見つけ

3 3 應用問題 一元一次方程式 題庫 Camdemy

一元一次方程式應用問題4速率問題 Youtube

今回は、 「1次関数の文章問題」 をやるよ。 携帯電話の料金プランや、電気・ガス・水道代の料金プランなど、実は身近なところで1次関数の式y＝ax＋bが使われているんだ。 例えば、次のような問題が1次関数を使う文章問題の代表例だよ。このように3つ文字を含むような連立方程式のことを、連立3元1次方程式といいます。 この場合には、 文字を1つずつ消去して解いていきましょう。 まずは、最初に消去する文字を決めます。 係数が揃ってる、揃えやすそうな文字から消去していきましょう。解けない5次方程式にも実は解法があった？ 方程式が「解けない」とはどういう意味なのか 話題の「三体問題」にも関係しています 浅田 秀樹

F1 C6 鸡兔同笼标准解法3 一元一次方程式 Youtube

中学数学 １次方程式 文章題の解き方 代金 個数

N 元連立1 次方程式 m n 行列の簡約化 行列の行基本変形 m n 行列で 操作I(i,a) i 行目に定数a をかける(a ̸= 0) 操作II(i,j,b) i 行目にj 行目のb 倍を加える 操作III(i,j) i 行目とj 行目を入れ替える https//bitly/rrmatrix (全学認証)高橋線形定理41 拡大係数行列に行基本変形を行っても, 対応する連立1次方程式2年生 2 連立方程式 知識・技能の習得を図る問題 年 組 号氏名 練習問題① 1 解が（x ，y ）＝（－1，4）になる連立二元一次方程式を1つつくりなさい。 2 解が（x ，y ）＝（2，1）になる連立方程式を次のアからオの中からすべて選びなさい。 ア 2x ＋y ＝1 イ 3x ＋4y ＝10 ウ 2x －3y ＝7 中学数学 1次方程式の文章題。 8回目は「割合の問題」解き方のコツです。 「定価や利益や割引の計算がわからない」 「食塩水の百分率って苦手」 「増減問題ができない」 これらすべてをこの記事でぜんぶ解決します。

無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア

二元一次方程各类应用题 松鼠文库

ベストオブ一次方程式問題集 ぬりえ壁紙hd

中学数学1年 1次方程式の利用 整数 受験の月

隨筆誌 一下1 2解二元一次聯立方程式 指數問題

初中數學重點突破 一元一次方程相關的6類問題 含例題和解析 每日頭條

隨筆誌 一上3 3一元一次方程式應用問題 正六邊形的周長問題

方程式の解き方 簡単な問題で 解き方のコツを覚えよう 中学や高校の数学の計算問題

中学数学 一次方程式

1 次方程式問題 シモネタ

01一元一次方程的概念一元一次方程初中数学初一 Youtube

初中数学 二元一次方程 特别需要注意的问题 考生最好看看 每日头条

２元１次方程式 無料で使える中学学習プリント

中学1年生 数学 無料問題集 一次方程式 おかわりドリル

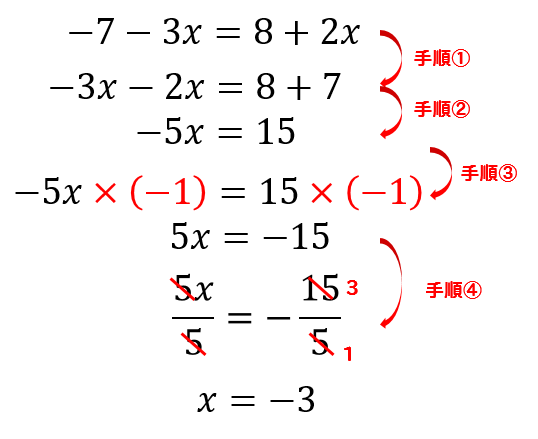
中１方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ

中学３年生 数学 ２次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

連立２元１次方程式を自由に解こう 中学2年生の数学 身勝手な主張

一元一次方程式應用問題 Shareclass

一次方程式とは 慶應生が解き方3ステップ教えます 問題 文章題付き 高校生向け受験応援メディア 受験のミカタ

最も欲しかった 数学2 次方程式 ニスヌーピー壁紙

三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org

國中數學的一元一次方程式筆記 Clear

一元一次方程式的應用3 應用問題1 2 解的合理性 Ppt Download

一元一次方程式應用題 1 1 2 Youtube

中3 二次方程式の解き方 平方根 因数分解 中学数学の方程式 中間 期末テスト 高校入試対策

解一元一次方程計算題每天訓練 15分鐘 每日頭條

解二元一次方程 典型解答题的分析方法及切入点 每日头条

一次方程式の解の求め方 数学fun

一次方程式 中1 練習問題あり答えあり 中学生 数学のノート Clear

求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博

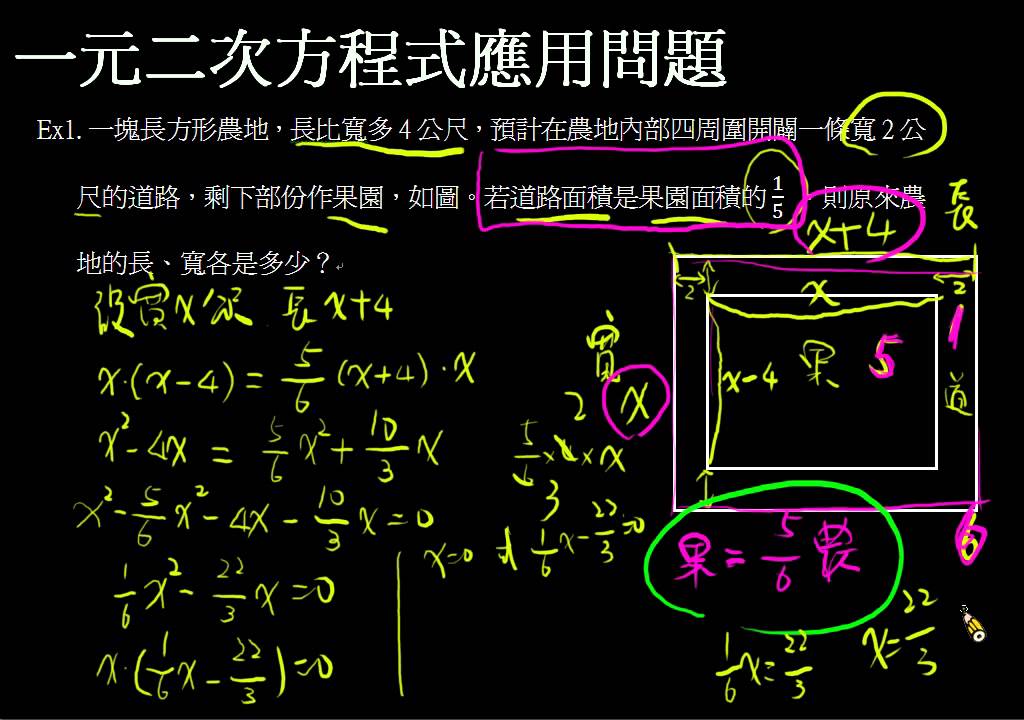
一元二次方程式應用問題 例1 2 已下架內容 均一教育平台

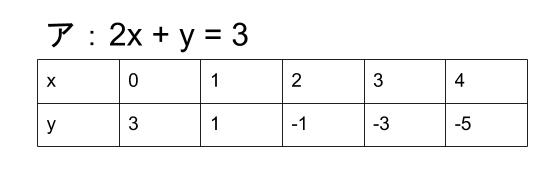
中学数学 ２元１次方程式と連立方程式 中学数学の無料オンライン学習サイトchu Su

最も共有された 1 次方程式分数 シモネタ

１次方程式の解き方２ 無料で使える中学学習プリント

中学数学 １次方程式 文章題の解き方 速さ 時間 道のり

一般 一元一次式 加快速度 已下架內容 均一教育平台

求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博

1 次方程式問題 シモネタ

中学数学1年 1次方程式の利用 分配と過不足 受験の月

國中數學解一元一次方程式 物以類聚篇 Youtube

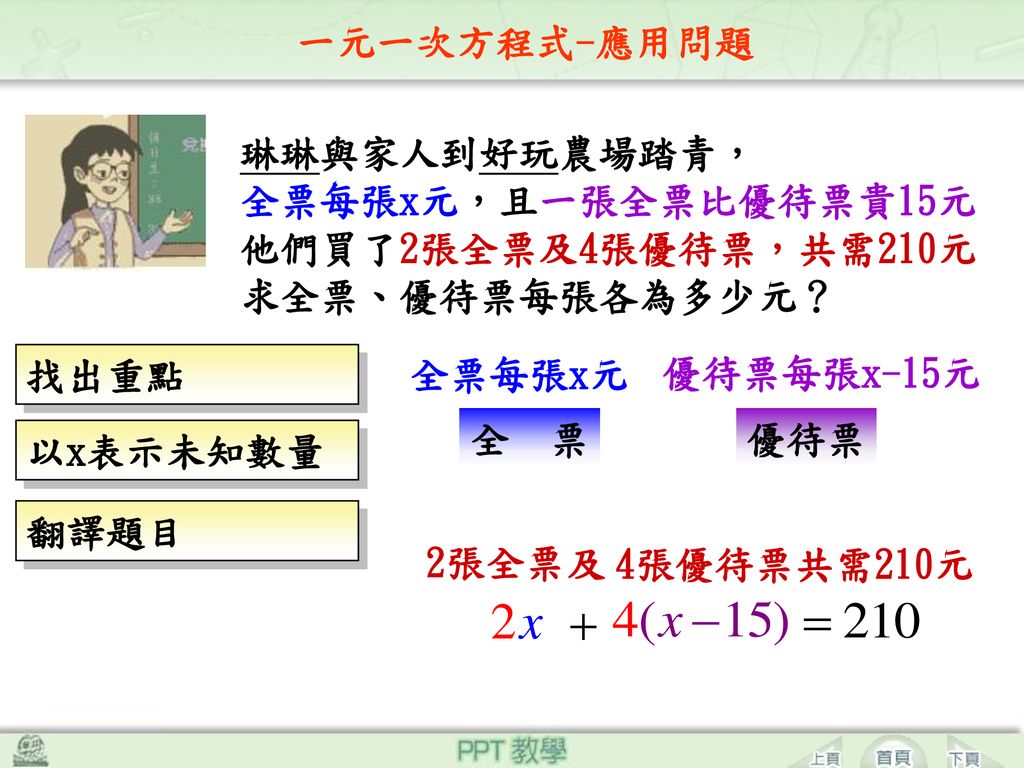
一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

二元一次方程式應用問題2 Youtube

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

1

Q Tbn And9gctdm2ioiwx1ofwk6oxyprfslnkssmzd2jo K6eubdtv2cctnoej Usqp Cau

一次方程式の文章題1 数 代金 過不足の問題 無料で使える中学学習プリント

0以上2 次方程式問題 シモネタ

一次方程式の問題や文章題の解き方を例題で詳しく解説 Studyplus スタディプラス

無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア

二元一次聯立方程式應用問題例4 5 Youtube

Star Lesson 3 3 一元一次方程式 應用題01 考古題解 Youtube

中学数学 １次方程式 文章題の解き方 代金 個数

中学３年生 数学 ２次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

國一下1之3 二元一次應用問題演練11 濃度問題uuu 108課綱未來教育x凱爺數學 Youtube

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

連立２元１次方程式を自由に解こう 中学2年生の数学 身勝手な主張

二元一次方程式應用問題1 Youtube

109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass

一元一次方程式應用問題 翰林雲端學院

無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア

一次方程式の問題や文章題の解き方を例題で詳しく解説 Studyplus スタディプラス

一元一次方程式的解题方法与技巧 自学习网

一元一次方程知识讲解 经典例题讲解 每日头条

隨筆誌 一上3 3一元一次方程式應用問題 父子年齡等差問題

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

初中數學一元一次方程含參數問題的解題策略 不容錯過 收藏 每日頭條

七年级下 数学实际问题与二元一次方程组题型归纳 含练习题答案 七年级 老杨的博客

二元一次方程各类应用题 松鼠文库

方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく

一元二次方程式 懶人包

方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく

解一元一次方程計算題每天訓練 15分鐘 每日頭條

基測數學 96v1 單選24 二元一次方程式的應用問題 評量專區 均一教育平台

一元一次方程式應用問題 Shareclass

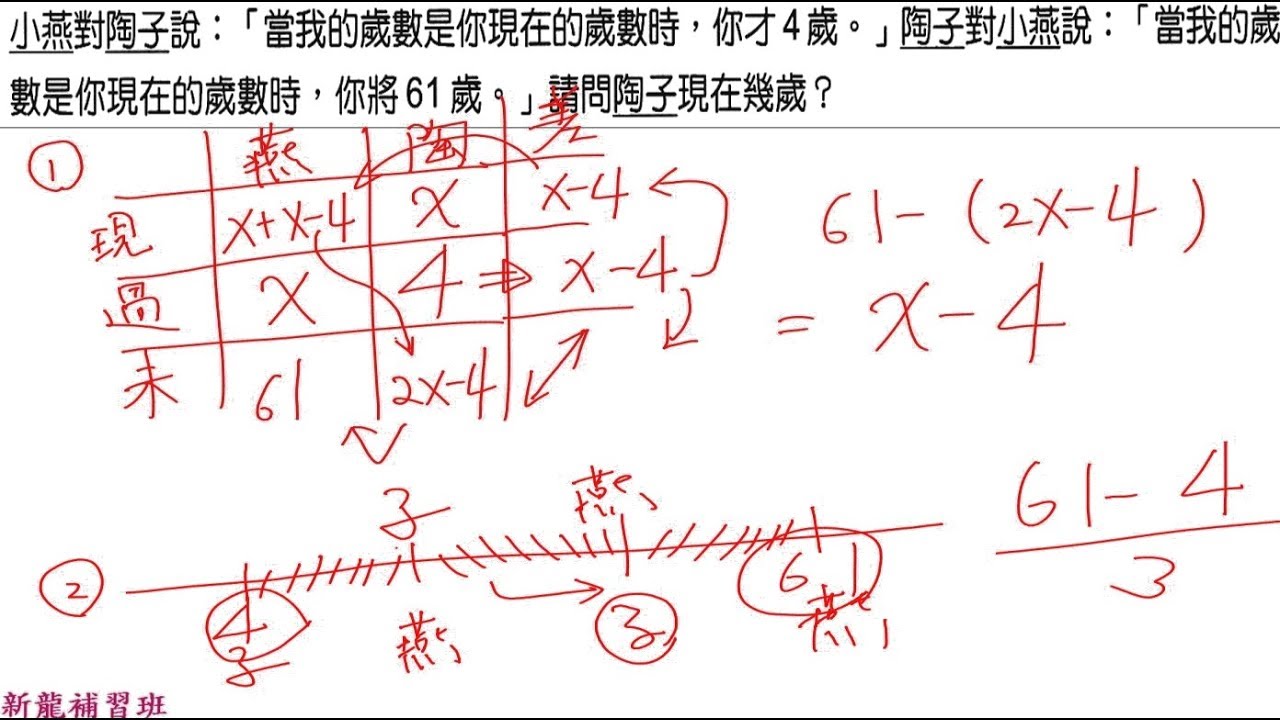
7年級上數學 一元一次方程式 年齡問題 Vs 小學算術解法 17 07 08 Youtube

中学1年生 数学 無料問題集 一次方程式 おかわりドリル

名師課輔網 一元一次方程式應用問題人數

三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org

方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく

1

一元一次方程式的應用3 應用問題1 2 解的合理性 Ppt Download

解一元二次方程式 明誠中學程式設計學習網

１次方程式の解の利用 無料で使える中学学習プリント

一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download

中学1年生 数学 無料問題集 一次方程式 おかわりドリル